Irrational Numbers
Irrational Numbers: Overview
This topic covers concepts such as Irrational Numbers, Need for Irrational Numbers, Real Numbers, Unique Representation of Real Numbers on Number Line, Representation of Irrational Numbers on Number Line, etc.
Important Questions on Irrational Numbers
Locate on the number line, the point representing the number .
The combination of rational and irrational number is called _____ number.
Which of the following is an irrational number?
Which of these is an irrational number?
Find the length of the diagonal of a unit square and classify it as rational or irrational number.
The length of the diagonal of a unit square is a rational number.
Prove that the length of the diagonal of a unit square is an irrational number.
The decimal expansion of an _____ number is non-terminating and non-repeating.
The decimal representation of the rational number is
Which of the following is not an irrational number?
What is an irrational number? Give an example.
The length of the diagonal of a square having sides of unit length is a irrational number.
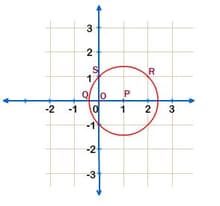
In the graph below, is the centre of the circle. and are two points on the circle.
What is the -coordinate of point Q?
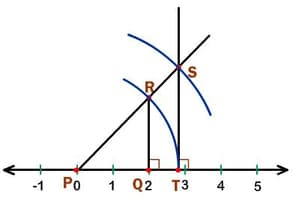
On the number line shown below,
1) $ \overline{\text{PQ}}$ = $ \overline{\text{QR}}$, with $ \overline{\text{PQ}}$⊥$ \overline{\text{QR}}$. Similarly,
2) $ \overline{\text{PT}}$ = $ \overline{\text{TS}}$, with $ \overline{\text{PT}}$⊥$ \overline{\text{TS}}$.
RT is an arc of radius PR and centre P. Another arc of radius PS and centre P, passes through S.
At which of the following points would the arc passing through point “S” intersect the number line?